
#문제1. response.csv파일 내 데이터에서 작업 유형에 따른 응답 정도에 차이가 있는가를 단계별로 검정
#1-1. 파일 가져오기
data <- read.csv("response.csv", header = TRUE)
head(data)
#1-2. 코딩변경(리코딩)
data$job2[data$job == 1] <-"학생"
data$job2[data$job == 2] <-"직장인"
data$job2[data$job == 3] <-"주부"
data$response2[data$response == 1] <-"무응답"
data$response2[data$response == 2] <-"낮음"
data$response2[data$response == 3] <-"높음"
#1-3. 교차분할표 작성
table(data$job2, data$response2)
#1-4. 동질성 검정
chisq.test(data$job2, data$response2)
'''X-squared = 58.208, df = 4, p-value = 6.901e-12'''
#1-5. 검정 결과 해석
#귀무가설 : 작업 유형에 따른 응답 정도에 차이가 없다.
#대립가설 : 작업 유형에 따른 응답 정도에 차이가 있다.
#카이제곱값: 58.208, p-value : 6.901e-12로,
#신뢰수준 95%하에서 자유도 4의 카이제곱 확률은 9.488보다 크며
#p-value는 0.05보다 작으므로 대립가설이 채택된다.
#문제2. attitude 데이터를 이용하여 등급(rating)에 영향을
# 미치는 요인을 회귀를 이용해 식별하고 후진제거법을
# 이용하여 적절한 변수 선택을 하여 최종 회귀식을 구하시오.
#2-1. 데이터 가져오기
data2 <- (attitude)
head(data2)
#2-2. 회귀분석 실시
ss <- lm(rating ~ ., data = data2)
ss
#2-3. 수행결과 산출 및 해석
summary(ss)
#p-value를 보았을 때 통계적으로 유의함을 알 수 있다.
#2-4. 후진제거법을 이용하여 독립변수 제거
ss2 <- step(ss, direction = "backward")
formula(ss2)
#learning 과 complaints 두 개만 남았다.
#2-5. 최종 회귀식
ss2
Y = 9.8709 + (0.6435 * complaints) + (0.2112 * learning)
#문제3. cleanData.csv 파일 내 데이터에서 나이와 직위간의 관련성을 단계별로 분석
#3-1. 파일 가져오기
data3 <- read.csv("cleanData.csv")
head(data3)
#3-2. 코딩 변경(변수 리코딩)
x <- data3$position
y <- data3$age3
#3-3. 산점도를 이용한 변수간의 관련성 보기
plot(x,y)
#3-4. 독립성 검정
library(ggplot2)
library(gmodels)
CrossTable(x, y, chisq = TRUE)
#3-5. 결과 해석
#귀무가설 : 나이와 직위간의 관련성이 없다.(독립적이다)
#대립가설 : 나이와 직위간의 관련성이 있다.(독립적이지 않다.)
#p-value = 1.548058e-57로 통계적으로 유의하다.
#Chi^2 = 287.8957로 자유도 8, 유의수준 0.05의 카이제곱 15.507보다 크다.
#따라서 대립가설 채택. 나이와 직위간 관련성이 있다.
#문제 4. mtcars 데이터에서 엔진(vs)을 종속변수로, 연비(mpg)와
# 변속기종류(am)를 독립변수로 설정하여 로지스틱 회귀분석 실시
#4-1. 데이터 가져오기
data4 <- (mtcars)
head(data4)
dim(data4)
str(data4)
#4-2. 로지스틱 회귀분석 실행하고 회귀모델 확인
#변수 선택
cars_df <- data4[, c(1, 8, 9)]
str(cars_df)
#로지스틱 회귀분석 실행 및 회귀모델 확인
cars_model <- glm(vs ~., data = cars_df, family = 'binomial', na.action = na.omit)
cars_model
#4-3. 로지스틱 회귀분석 요약정보 확인
summary(cars_model)
'''> summary(cars_model)
Call:
glm(formula = vs ~ ., family = "binomial", data = cars_df, na.action = na.omit)
Deviance Residuals:
Min 1Q Median 3Q Max
-2.05888 -0.44544 -0.08765 0.33335 1.68405
Coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) -12.7051 4.6252 -2.747 0.00602 **
mpg 0.6809 0.2524 2.698 0.00697 **
am -3.0073 1.5995 -1.880 0.06009 .
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
(Dispersion parameter for binomial family taken to be 1)
Null deviance: 43.860 on 31 degrees of freedom
Residual deviance: 20.646 on 29 degrees of freedom
AIC: 26.646
Number of Fisher Scoring iterations: 6'''
#4-4. 로지스틱 회귀식
formula(cars_model)
"vs ~ mpg + am"
#in(odds) = -12.7051 + (0.6809 * mpg) + (-3.0073 * am)
#in odds 회귀식을 구한 다음에 4-5를 계산할 수 있음.
#4-5. mpg가 30이고 자동변속기 (am=0)일 때 승산 (odds)?
y = -12.7051 + (0.6809 * 30) + (-3.0073 * 0)
exp(odds)
#문제 5. 새롭게 제작된 자동차의 성능(주행거리(마일)/갤런)을 -30도,
# 0도, 30도의 기온 하에 성능을 측정하였다.
# 각 기온당 측정된 성능데이터의 수는 4개였다.
# 성능데이터로부터 다음의 ANOVA 테이블을 구성하였다.
# 빈칸에 들어갈 숫자(정수)와 숫자를 계산한 식을 제시하시오.
#(a) : SStr = 72 (Mstr = SStr / k-1 )
#(b) : k-1 = 2
#(c) : Mstr = 36 ((10.8(F VALUE) = Mstr / 3.3334(MSE))
#(d) : SSE = 30 (3.3334(MSE) = SSE / 9(N-K))
#(e) : N-K = 9
#(f) : SST = SSE + SSTR = 102
#(g) : N-1 = 11** anova table
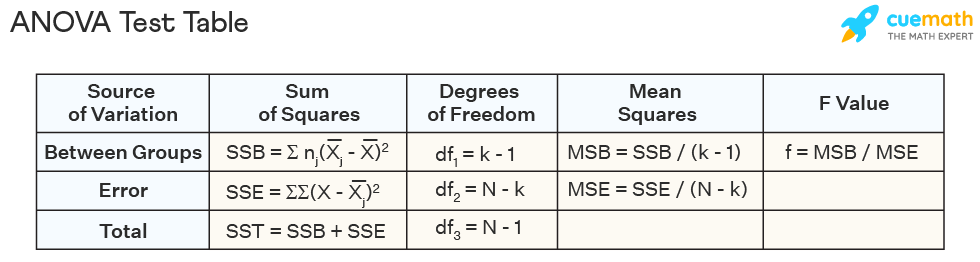
k = number of factor
N = data 의 수 (index, factor 제외하고)
'R > 연습문제 풀이' 카테고리의 다른 글
| [R] 다중 회귀분석 (0) | 2023.01.17 |
|---|---|
| [R] 요인 분석 (0) | 2023.01.17 |
| [R] 교차 분할표 / 카이제곱 분포 / 독립성 검정 (0) | 2023.01.17 |
| [R] 독립 표본 T 검정 / 두 집단 비율 검정 / 비모수 검정 / 단일 표본 대상 기술통계량(단측 가설 검정) (0) | 2023.01.17 |
| [R] 기술통계 / 범주화 / 교육 방법에 따른 시험 성적 차이 검정 (2) | 2023.01.17 |


댓글